LaTeX templates and examples — Physics
Recent

Detailed notes

Chapitre 2, Peip2, Polytech'Nice Sophia, sans les sch\'emas et applications sch\'ematis\'ees
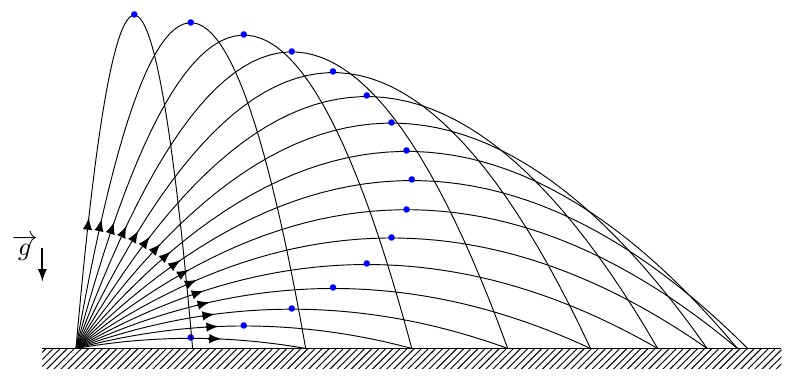
Ce document regroupe les codes TIKZ des figures utilisées pour le cours "PROBLEMES DE CHUTE" situé à la page http://femto-physique.fr/mecanique/meca_C3.php

Experimentalphysik 6: Festkörperphysik

Experimentalphysik 5: Kern- und Teilchenphysik

This is the template used in Physics 211 (calculus-based mechanics) as taught at Cortland High School in Cortland, NY. The abstract should be a short 3-5 sentence paragraph. In it, you should state the hypothesis, what you did, and what you found. The abstract is meant to be a very short summary of your paper to follow. It is a good suggestion to write the abstract last in your report after you have written everything else. This will allow you to best summarize your work.

Experimentalphysik 5: Kern- und Teilchenphysik
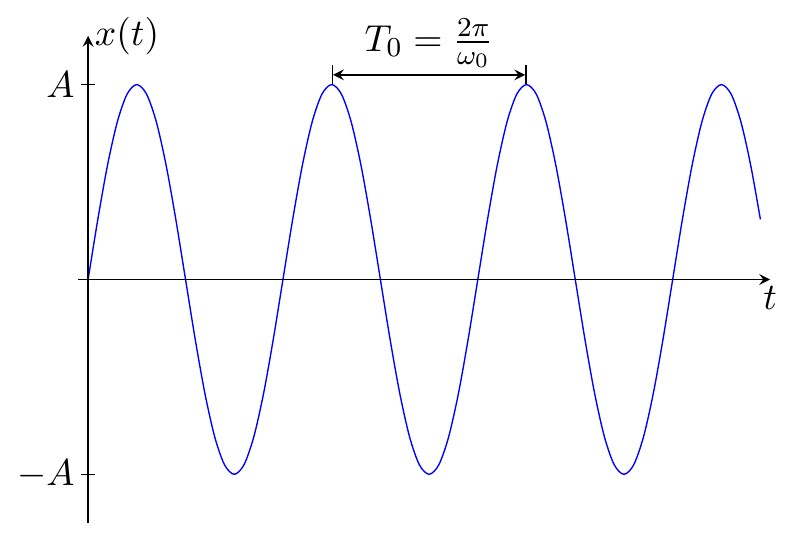
Ce document regroupe les codes TIKZ des figures utilisées pour le cours "Oscillateurs Mécaniques" situé à la page http://femto-physique.fr/mecanique/meca_C4.php

Scientific investigation
\begin
Discover why over 25 million people worldwide trust Overleaf with their work.