overleaf template galleryLaTeX templates and examples — Recent
Discover LaTeX templates and examples to help with everything from writing a journal article to using a specific LaTeX package.
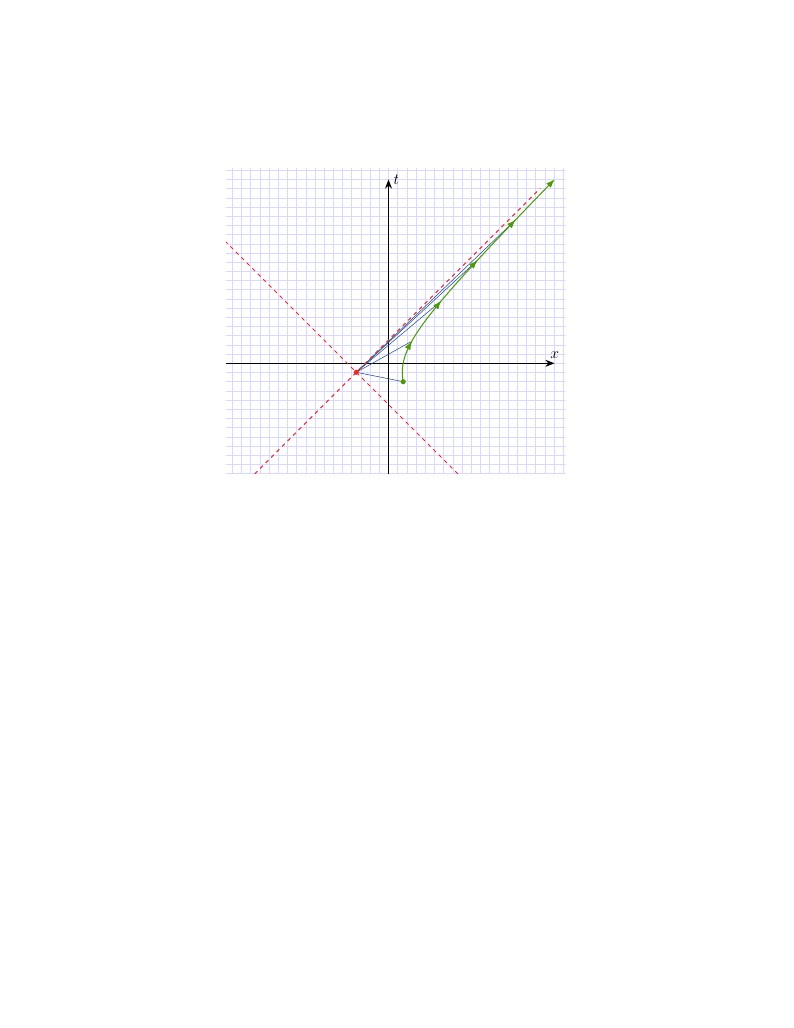
Use TikZ/PGF to programmatically draw spacetime diagrams for uniformly accelerated observers. Set the acceleration, initial conditions, and other parameters. Questions/Comments to Robert McNees at rmcnees@luc.edu, http://jacobi.luc.edu January 2015

This example from section three of the LaTeX verse package documentation demonstrates an ambitious use of \indentpattern to create a striking visual effect. In this case it is defined to recreate the famous typesetting of the original Mouse's Tale as it appeared in print. Background: "The Mouse's Tale" is a poem by Lewis Carroll involving a 'quadruple pun' which appears in his novel Alice's Adventures in Wonderland. It uses typesetting style to create the final pun (it is a mouse's tale typeset in the shape of a mouse's tail). For more details see the poem's Wikipedia entry.

Simple problem set involving complex numbers.

Fakulteta za organizacijske vede, Univerza v Mariboru - predloga zaključnega dela, UM FOV

In recent years, interest in optical wireless(OW) as a promising complementary technology for RF technology has gained new momentum fueled by significant deployments in solid state lighting technology. This article aims at reviewing and summarizing recent advancements in Short Range Optical Wireless communication, with the main focus on indoor deployment scenarios. This includes a discussion of challenges, potential applications,state of the art, and prospects. We discuss exclusively about the deployment of OWC technique using the existing infrastructure such as LED lighting fixtures, mobile phone cameras and flashes, and headlamps of vehicles, with little or no add-ons, which in turn will enable Internet of Things (IoT). This paper also discusses the challenges and potential of Optical Wireless Communication.
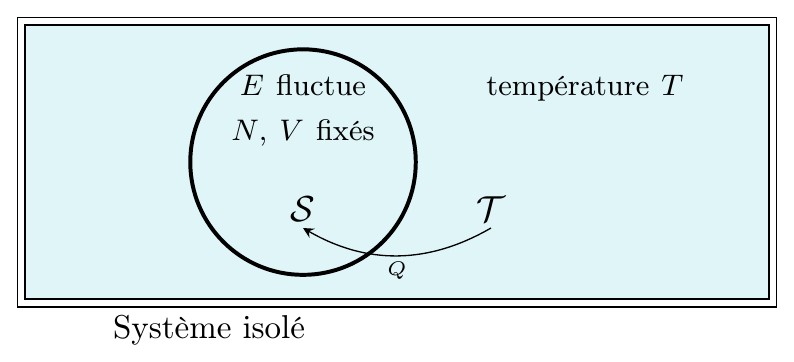
Ce document regroupe les codes TIKZ des figures utilisées pour le cours "Systèmes en équilibre thermique" situé à la page http://femto-physique.fr/physique_statistique/phystat_C2.php

homework on quantum mechanics course

Resuelva la ecuación

homework 11W
\begin
Discover why over 25 million people worldwide trust Overleaf with their work.